Delong检验

一、Delong检验的作用

用于比较两个ROC曲线的性能，Delong检验是用于AUC面积的显著性检验的。如果两个模型的AUC大小有异但是没有通过Delong检验，那么也不能说明这两个模型有显著的不同。

总之，Delong检验就是一种统计学上用于检验AUC显著性的检验方法。

二、Delong检验的原理

Delong检验本质上是构造一个变量，这个变量涉及了用于比较的两个AUC值，并且是服从或近似服从正态分布的。然后利用正态分布对其做一个假设检验。

1.符号参数的解释

符号	含义
m	实际正类数量
n	实际负类数量
	模型A中，正类样本被识别为正类的概率(分数)
	模型B中，负类样本被识别为正类的概率(分数)
	估计AUC

2. AUC的计算

这个公式的简单理解见下图
)

当 X < Y 时，说明模型负类被预测为正类的概率大于正类被预测为正类的概率，因此我们惩罚模型不良预测使AUC + 0
当 X > Y 时，说明模型负类被预测为正类的概率小于正类被预测为正类的概率，模型进行了良好的预测，因此对模型进行奖励使得AUC + 1/mn
当 X = Y 时，说明以上两种可能性各占50%，因此给予AUC一半的分数，即AUC + 1/2mn

以上的解释只是一个简单的理解，这个估计AUC的期望的值等于ROC曲线中的面积计算得到的值，具体的数学推导我还没有找到。

[这里缺少一个数学证明]

3. 构造统计量进行检验

然后利用构造一个服从正态分布的统计量。这里用 表示模型A的经验AUC，用 表示模型B的经验AUC。

有统计量z：

这个z统计量是近似服从标准正态分布的。

[这里缺少一个数学证明]

检验的假设为 。
当 时，在显著性p<0.05的双边检验中，拒绝零假设，A，B两模型的AUC具有显著性差别。

4. 方差与协方差的计算

(1)方差计算

delong检验中的方差是通过分别计算正类和负类的方差，然后通过加权来得出最后的方差。
首先是定义了结构组件， 和 ，公式如下：

如图所示，图中的 的值为 ， 的值为 。

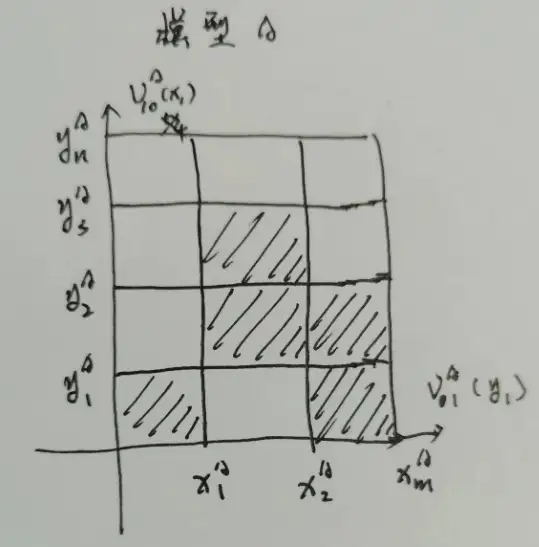
有了结构组件后，利用结构组件计算方差分量 的含义为A模型 10 部分的方差分量， 的含义为A模型 01 部分的方差分量，计算的公式为

然后进行加权相加，A模型的方差 为

B模型的计算相同

(2)协方差的计算

协方差的计算与方差类似，也是先计算分量，然后进行加权

---

参考链接

[1] 简述
[2] 算法
[3] Delong检验原理
[4] Delong检验具体例子
[5] Comparing Two ROC Curves-Paired Design

---