生存分析(1)_概念与原理
生存分析
生存分析的概念与作用
生存分析指的是根据调查或者实验得到的数据对样本的寿命进行分析和推断的一个分析过程。生存分析的结果往往是一幅以时间为横坐标,以生存概率为纵坐标的二维散点/折线图。其中每一个散点代表的是样本总体生存到某一时间点的概率。如下图所示。
生存分析的结果可以用于比较两组样本谁对研究对象有更好的寿命延长或减少效果。
生存分析的一些概念
- 总体生存期(Overall Survival): OS, 样本结局为死亡状态,这个死亡是任何原因导致的死亡都算,只关心是否死亡,不关心因为何种原因死亡。
- 无病生存期(Disease Free Survival): DFS, 经过治疗后未发现肿瘤,结局指标为“疾病复发或死亡”同样不关心死亡原因。
- 无进展生存期(Progression Free Survival): PFS, 指疾病经过治疗后,没有进一步恶化的生存期,结局指标为“发生恶化或死亡 ”。
Kaplan-Meier方法概念介绍
Kaplan-Meier是Kaplan与Meier在1958年提出的一种生存分析结果图绘制的计算方法。我们已经知道了生存分析结果图中的纵坐标是生存率,而如何计算这个生存率呢?这就是Kaplan-Meier方法所解决的。
| 时间(年) | 生存人数 | 死亡人数 |
|---|---|---|
| 1 | 30 | 0 |
| 2 | 28 | 2 |
| 3 | 25 | 3 |
| 4 | 23 | 2 |
| 5 | 21 | 2 |
| 6 | 17 | 4 |
| 7 | 15 | 2 |
| 8 | 12 | 3 |
如上表所示,生存人数表示在对应年份内研究的人群中尚存活的人数,死亡人数指的是在对应年份内研究人群中死亡的数量。那么在上表的数据样本下,我们应该如何计算人群存活到某一个时间点的概率呢?例如表中第4年生存率是多少?显然,如果我们要计算某人在时间为 4 时活着的概率,那么必然他在时间为 1,2,3 时均存活。即有:
而在 t=i 时不死亡的概率可以由 1 - P{在t=i时死亡} 求出。在上表的数据中,P{在t=i时死亡}的计算如下:
根据上述分析我们可以计算出样例数据,不同时间点的死亡概率和生存率。计算结果如下表
| 时间(年) | 生存人数 | 死亡人数 | 死亡率 | 生存率 |
|---|---|---|---|---|
| 1 | 30 | 0 | 0/30 = 0 | 1 |
| 2 | 28 | 2 | 2/28 = 0.07 | 0.93 |
| 3 | 25 | 3 | 3/25 = 0.12 | 0.82 |
| 4 | 23 | 2 | 2/23 = 0.08 | 0.75 |
| 5 | 21 | 2 | 2/21 = 0.09 | 0.68 |
| 6 | 17 | 4 | 4/17 = 0.23 | 0.52 |
| 7 | 15 | 2 | 2/15 = 0.13 | 0.45 |
| 8 | 12 | 3 | 3/12 = 0.25 | 0.34 |
以表中的 时间(年) 为横坐标, 生存率 为纵坐标即可以作出该表的生存曲线。
Logrank 检验
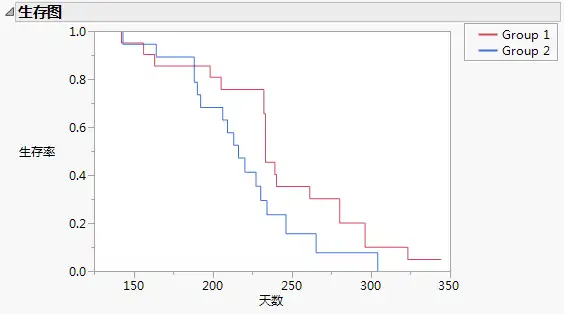
在生存分析中往往我们作出的图像中不止一条生存曲线,如下图所示:

而如何比较这两条生存曲线是否有统计学上的区别,就需要用到logrank检验。logrank 检验是一种非参数检验方法,中文名为时序检验。用于比较两条生存曲线是否有显著性差别。logrank检验的原假设是两生存曲线不存在统计学差异。logrank检验可以分为两类Z检验和
若原假设成立,那么Group1和Group2的实际死亡人数应当和基于两组样本计算出的死亡概率拟合出的理论死亡人数差距不大。即可以构造出如下的卡方值:
其中内层的三个求和号表示的是对时间求和,计算出样本的总实际死亡人数和总理论死亡人数。j 代表参与检验的组别数量,在两组别的比较中 j=2 。
其中
如果原假设成立,那么最后得到的卡方值不应过大,即对卡方值进行自由度为 Group数量-1 的检验。若卡方值足够大,则可以拒绝原假设,两组有统计学上的差异。
cox回归分析
以上的作图以及用logrank分析组别之间的统计学差异,只适用于某单一变量如:性别,生活区域,某基因的表达量等,基于这些变量进行分组。而在实际应用中往往需要考虑多组变量,这时候就要用到cox回归分析。
我们这里不展开讲cox回归模型的推导过程,简述一下结论,具体的推导过程见 [连接4]。首先是cox回归模型的公式:
其中,
在这个cox回归模型中,